Page 43 - 4128

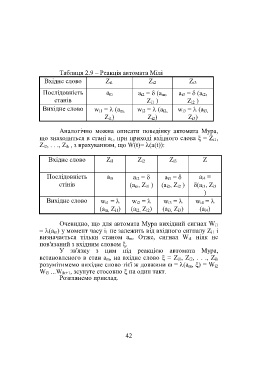
Таблиця 2.9 – Реакція автомата Мілі
Вхідне слово Z i1 Z i2 Z i3

Послідовність a m a i2 =  (a m, a i3 =  (a i2,
станів Z i1 ) Z i2 )
Вихідне слово w i1 =  (a m, w i2 =  (a i2, w i3 =  (a i3,
Z i1) Z i2) Z i3)

Аналогічно можна описати поведінку автомата Мура,
що знаходиться в стані a 1, при приході вхідного слова  = Z i1,
Z i2, . . ., Z ik , з врахуванням, що W(t)= (а(t)):

Вхідне слово Z i1 Z i2 Z i3 Z

Послідовність a m a i2 =  a i3 =  a i4 =
стінів (a m, Z i1 ) (a i2, Z i2 ) (a i3, Z i3
)
Вихідне слово w i1 =  w i2 =  w i3 =  w i4 = 
(a m, Z i1) (a i2, Z i2) (a i3, Z i3) (a i4)

Очевидно, що для автомата Мура вихідний сигнал W i1
= (a m) у момент часу i 1 не залежить від вхідного сигналу Z i1 і
визначається тільки станом a m. Отже, сигнал W i1 ніяк не
пов'язаний з вхідним словом .
У зв'язку з цим під реакцією автомата Мура,
встановленого в стан a m, на вхідне слово  = Z i1, Z i2, . . ., Z ik
розумітимемо вихідне слово тієї ж довжини  = (a m, ) = W i2
W i3 ...W ik+1, зсунуте стосовно  на один такт.
Розглянемо приклад.

42